Worked Example
This example was taken from the talk "A Unified Proof System for Discrete Combinatorial Problems" at slide 58 by Jakob Nordström.
Input
For this example, with constraints over variables \(w,x,y,z\), we will have three input axioms:
- \( w + 2x + y \ge 2 \)
- \( w + 2x + 4y + 2z \ge 5 \)
- \( \overline{z} \ge 0 \)
example (xs : Fin 4 → Fin 2)
(c1 : PBIneq ![(1,0),(2,0),(1,0),(0,0)] xs 2)
(c2 : PBIneq ![(1,0),(2,0),(4,0),(2,0)] xs 5)
(c3 : PBIneq ![(0,0),(0,0),(0,0),(0,1)] xs 0)
Goal
The objective of this example is to prove: \[ w + 2x + 2y \ge 3 \]
: PBIneq ![(1,0),(2,0),(2,0),(0,0)] xs 3 := by
Execution
We start by using muliplication of the first constraint by 2: \[ \frac {w + 2x + y \ge 2} {2w + 4x + 2y \ge 4} (\text{Multiply by 2}) \]
let t1 : PBIneq ![(2,0),(4,0),(2,0),(0,0)] xs 4 := by apply Multiplication c1 2
Now we add this result to constraint 2: \[ \frac {{2w + 4x + 2y \ge 4}\qquad {w + 2x + 4y + 2z \ge 5}} {3w + 6x + 6y + 2z \ge 9} (\text{Add}) \]
let t2 : PBIneq ![(3,0),(6,0),(6,0),(2,0)] xs 9 := by apply Addition t1 c2
At this point we want to remove the variable \(z\), as it does not appear in our goal. Then we will use c3 \(\overline{z} \ge 0\) then multiply it by 2: \[ \frac {\overline{z} \ge 0} {2\overline{z} \ge 0} (\text{Multiply by 2}) \]
let t3 : PBIneq ![(0,0),(0,0),(0,0),(0,2)] xs 0 := by apply Multiplication c3 2
Performing addition will cancel out the \(z\) variable: \[ \frac {{3w + 6x + 6y + 2z \ge 9}\qquad {2\overline{z} \ge 0}} {3w + 6x + 6y \ge 7} (\text{Add}) \]
let t4 : PBIneq ![(3,0),(6,0),(6,0),(0,0)] xs 7 := by apply Addition t2 t3
And lastly a division by 3 is performed to arrive at the goal: \[ \frac {3w + 6x + 6y \ge 7} {w + 2x + 2y \ge 3} (\text{Divide by 3}) \]
exact Division t4 3
done
Summarizing, this is the full proof:
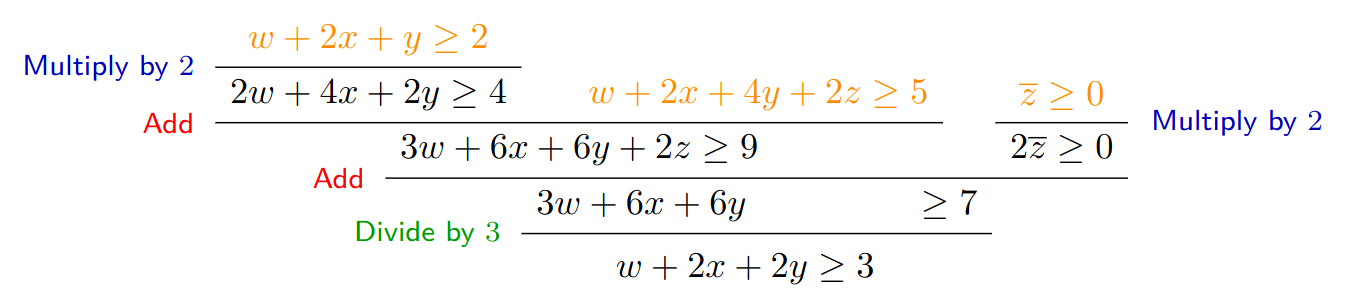
example
(xs : Fin 4 → Fin 2)
(c1 : PBIneq ![(1,0),(2,0),(1,0),(0,0)] xs 2)
(c2 : PBIneq ![(1,0),(2,0),(4,0),(2,0)] xs 5)
(c3 : PBIneq ![(0,0),(0,0),(0,0),(0,1)] xs 0)
: PBIneq ![(1,0),(2,0),(2,0),(0,0)] xs 3
:= by
let t1 : PBIneq ![(2,0),(4,0),(2,0),(0,0)] xs 4 := by apply Multiplication c1 2
let t2 : PBIneq ![(3,0),(6,0),(6,0),(2,0)] xs 9 := by apply Addition t1 c2
let t3 : PBIneq ![(0,0),(0,0),(0,0),(0,2)] xs 0 := by apply Multiplication c3 2
let t4 : PBIneq ![(3,0),(6,0),(6,0),(0,0)] xs 7 := by apply Addition t2 t3
exact Division t4 3
done