Cutting Planes with Lean 4
by Bernardo Borges
This book is the official documentation for the usage of the lean-cutting-planes library. It is currently a work in progress, with the goal to provide full expressivity in Lean 4 for the cutting planes formal logic.
Future work in this project will aim to verify unsat demonstrations that were produced by solvers suchs as RoundingSat and check that their reasoning was correct.
Introduction
Cutting Planes and Lean 4
Cutting Planes is a method in mathematical optimizaiton used in the context of discrete combinatorial problems, that can be applied in Software testing, Formal verification and Proof logging. Pseudo-Boolean in the other hand is a logic system introduced by Jakob Nordström in his paper A Unified Proof System for Discrete Combinatorial Problems, which this project aims to implement and verify. Our proofs will consist of Pseudo-Boolean Constraints, that are 0-1 integer linear inequalities. Without loss of generality, we will use the normalized form.
\[ \sum_i{a_i l_i} \ge A \] Where we have:
- constant \( A \in \mathbb{N} \)
- coefficients \( a_i \in \mathbb{N} \)
- literals \( l_i: x_i\ \text{or}\ \overline{x_i}\ (\text{where } x_i + \overline{x_i} = 1) \)
- variables \( x_i \) take values \( 0 = false \) or \( 1 = true \)
In this regard, Pseudo-Boolean Reasoning works on two axioms and four rules, each of which are formally verified in this project using Lean 4
Lean 4 is a theorem prover and programming language developed by Leonardo de Moura. In the last years it became proeminent in the mathematics community, after Kevin Buzzard's The Xena Project of Imperial College London was formed, aiming to formalize all undergraduate level math, Peter Scholze's proof in the area of condensed mathematics called Liquid Tensor Experiment was formalized in 2021 and in 2023 Terence Tao used Lean to formalize a proof of the Polynomial Freiman-Ruzsa (PFR) conjecture, published in the same year.
Armed with a Lean 4 proof of the reasoning rules, complex proofs that involve these steps can be guaranteed to be correct.
Pseudo Boolean Rules
Interaction
As a starting point for the pseudo boolean reasoning we will get constraints from the user, which are subject to a normalization process. Then the rules can be applied to produce further inequalities \[ xs := [0,1] \]
\[ as := [(1,0),(2,0)] \equiv x + 2y \]
\[ bs := [(0,3),(2,0)] \equiv 3 \overline{x} + 2y \]
\[ {{c1 := \sum_i{as_i xs_i} \ge 2}\qquad {c2 := \sum_i{bs_i xs_i} \ge 5}} \]
def xs : Fin 2 → Fin 2 := ![0,1]
def c1 : PBIneq ![(1,0),(2,0)] xs 2
def c2 : PBIneq ![(0,3),(2,0)] xs 5
Addition Rule
Two constraints can be added together, adding the coefficients and the constants. Another behaviour is that \(x_i\) and \(\overline{x_i}\) that may appear together cancel each other: \[ \frac {{\sum_i{a_i l_i} \ge A}\qquad {\sum_i{b_i l_i} \ge B}} {\sum_i{(a_i + b_i) l_i} \ge (A+B)} \]
def xs : Fin 2 → Fin 2 := ![0,1]
def c1 : PBIneq ![(1,0),(2,0)] xs 2
def c2 : PBIneq ![(0,3),(2,0)] xs 5
-----------------------------------
def c3 : PBIneq ![(0,2),(4,0)] xs 6 := by apply Addition c1 c2
Multiplication Rule
A constraint can be multiplied by any \( c \in \mathbb{N}^{+} \): \[ \frac {\sum_i{a_i l_i} \ge A} {\sum_i{c a_i l_i} \ge c A} \]
def xs : Fin 2 → Fin 2
def c1 : PBIneq ![(1,0),(2,0)] xs 2
-----------------------------------
def c2 : PBIneq ![(2,0),(4,0)] xs 4 := by apply Multiplication c1 2
Division Rule
A constraint can be divided by any \( c \in \mathbb{N}^{+} \), and the the ceiling of this division in applied: \[ \frac {\sum_i{a_i l_i} \ge A} {\sum_i{ \lceil \frac{a_i}{c} \rceil l_i} \ge \lceil \frac{A}{c} \rceil} \]
def xs : Fin 2 → Fin 2
def c1 : PBIneq ![(3,0),(6,0)] xs 7
-----------------------------------
def c2 : PBIneq ![(1,0),(2,0)] xs 3 := by apply Division c1 3
Saturation Rule
A constraint can replace its coefficients by the minimum between them and the constant: \[ \frac {\sum_i{a_i l_i} \ge A} {\sum_i{ \min(a_i,A)\cdot l_i} \ge A} \]
def xs : Fin 2 → Fin 2
def c1 : PBIneq ![(3,0),(6,0)] xs 3
-----------------------------------
def c2 : PBIneq ![(3,0),(3,0)] xs 3 := by apply Saturation c1
All these rules can be seen in practice in the Worked Example
Worked Example
This example was taken from the talk "A Unified Proof System for Discrete Combinatorial Problems" at slide 58 by Jakob Nordström.
Input
For this example, with constraints over variables \(w,x,y,z\), we will have three input axioms:
- \( w + 2x + y \ge 2 \)
- \( w + 2x + 4y + 2z \ge 5 \)
- \( \overline{z} \ge 0 \)
example (xs : Fin 4 → Fin 2)
(c1 : PBIneq ![(1,0),(2,0),(1,0),(0,0)] xs 2)
(c2 : PBIneq ![(1,0),(2,0),(4,0),(2,0)] xs 5)
(c3 : PBIneq ![(0,0),(0,0),(0,0),(0,1)] xs 0)
Goal
The objective of this example is to prove: \[ w + 2x + 2y \ge 3 \]
: PBIneq ![(1,0),(2,0),(2,0),(0,0)] xs 3 := by
Execution
We start by using muliplication of the first constraint by 2: \[ \frac {w + 2x + y \ge 2} {2w + 4x + 2y \ge 4} (\text{Multiply by 2}) \]
let t1 : PBIneq ![(2,0),(4,0),(2,0),(0,0)] xs 4 := by apply Multiplication c1 2
Now we add this result to constraint 2: \[ \frac {{2w + 4x + 2y \ge 4}\qquad {w + 2x + 4y + 2z \ge 5}} {3w + 6x + 6y + 2z \ge 9} (\text{Add}) \]
let t2 : PBIneq ![(3,0),(6,0),(6,0),(2,0)] xs 9 := by apply Addition t1 c2
At this point we want to remove the variable \(z\), as it does not appear in our goal. Then we will use c3 \(\overline{z} \ge 0\) then multiply it by 2: \[ \frac {\overline{z} \ge 0} {2\overline{z} \ge 0} (\text{Multiply by 2}) \]
let t3 : PBIneq ![(0,0),(0,0),(0,0),(0,2)] xs 0 := by apply Multiplication c3 2
Performing addition will cancel out the \(z\) variable: \[ \frac {{3w + 6x + 6y + 2z \ge 9}\qquad {2\overline{z} \ge 0}} {3w + 6x + 6y \ge 7} (\text{Add}) \]
let t4 : PBIneq ![(3,0),(6,0),(6,0),(0,0)] xs 7 := by apply Addition t2 t3
And lastly a division by 3 is performed to arrive at the goal: \[ \frac {3w + 6x + 6y \ge 7} {w + 2x + 2y \ge 3} (\text{Divide by 3}) \]
exact Division t4 3
done
Summarizing, this is the full proof:
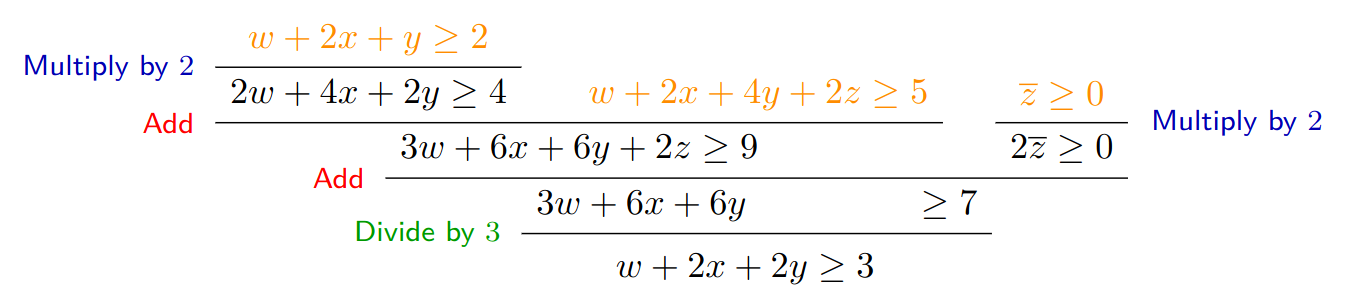
example
(xs : Fin 4 → Fin 2)
(c1 : PBIneq ![(1,0),(2,0),(1,0),(0,0)] xs 2)
(c2 : PBIneq ![(1,0),(2,0),(4,0),(2,0)] xs 5)
(c3 : PBIneq ![(0,0),(0,0),(0,0),(0,1)] xs 0)
: PBIneq ![(1,0),(2,0),(2,0),(0,0)] xs 3
:= by
let t1 : PBIneq ![(2,0),(4,0),(2,0),(0,0)] xs 4 := by apply Multiplication c1 2
let t2 : PBIneq ![(3,0),(6,0),(6,0),(2,0)] xs 9 := by apply Addition t1 c2
let t3 : PBIneq ![(0,0),(0,0),(0,0),(0,2)] xs 0 := by apply Multiplication c3 2
let t4 : PBIneq ![(3,0),(6,0),(6,0),(0,0)] xs 7 := by apply Addition t2 t3
exact Division t4 3
done